Most people know that adding up 0.1 + 0.2 equals 0.3. However computers represent it as 0.30000000000000004 .

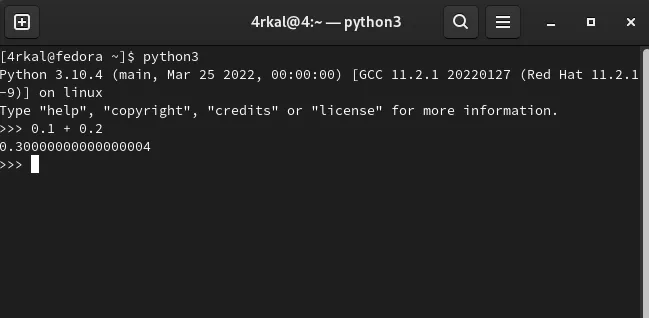
Here is a screenshot of it in python3 0.1+0.2 in python

Your first thought might be that this is just some kind of error. Well its not

Why does this happen?

Fractions can be represented precisely in the base 10 system (used by humans) if a prime factor of the base is used (10).

2 and 5 are the prime factors of 10.
1/2, 1/4, 1/5 (0.2), 1/8, and 1/10 (0.1) can be expressed precisely as a result of denominators use prime factors of 10.
Whereas, 1/3, 1/6, and 1/7 are repeating decimals as a result of denominators use a prime factor of 3 or 7. On the other hand, fractions can be represented precisely in the base 2 (binary) system (used by computers) if a prime factor of the base is used.
2 is the only prime factor of 2.
So 1/2, 1/4, 1/8 can all be expressed precisely because the denominators use prime factors of 2.
Whereas 1/5 (0.2) or 1/10 (0.1) are repeating decimals. When you perform math on these repeating decimals, you end up with leftovers which carry over when you convert the computer’s base-2 (binary) number into a more human-readable base-10 representation.

If you enjoyed this article consider donating

Why does this happen?¶